Poincaré-Hopf theorem
See @needham2021visual page 206.
Theorem
If a vector field $v$ on a smooth surface $S$ of genus $g$ has only a finite number of singular points $\{p_1,\cdots,p_n\}$ then the sum of their indices equal the Euler characteristic of the surface
$$ \sum_i \mathcal{J}_v(p_i)=\mathcal{X}(S)=2-2g $$$\blacksquare$
Proof
A wonderful proof is in @needham2021visual page 207
$\blacksquare$
As a immediate consequence, a vector field with no singular points can only exist in a surface of genus 0, i.e., in a topological torus

Another conclusion is the Hairy Ball Theorem.
And another conclusion is a proof for the generalized Euler formula (see @needham2021visual page 209):
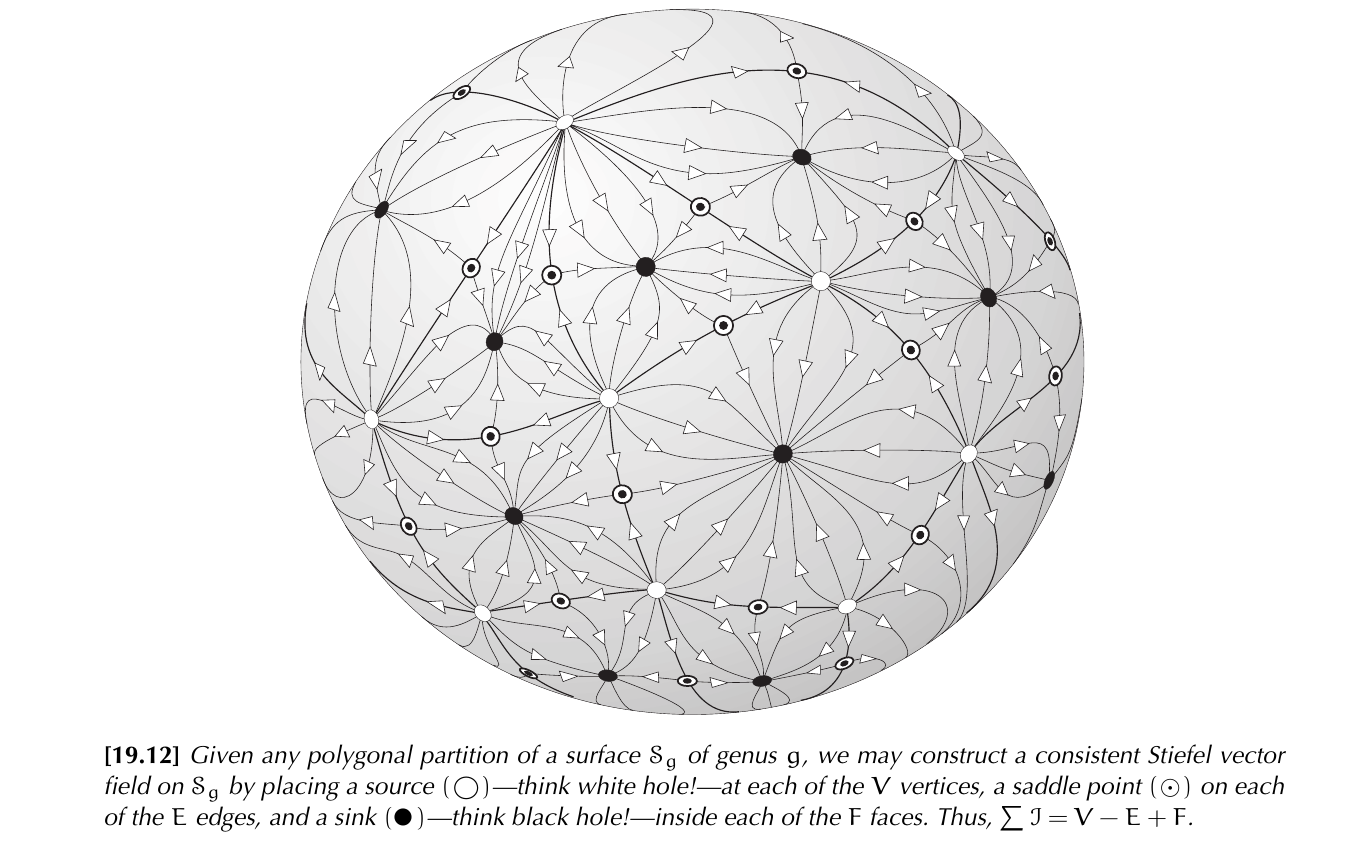
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: